Binary Search Tree

A binary search tree (BST) is a tree like data structure that is used for performing binary search. The core idea of a binary search tree is that binary search requires the data to be sorted first, which is time consuming, and it would be more efficient to store the data pre-sorted.

Note

Note that BSTs can only be used for data that is sortable. For the purposes of this lesson we assume that we are storing integers.

Recommended Video (6 minutes)

Concept

A BST is a tree where each node:

• contains the data (key) for that node

• references to two children: left and right

and satisfies the BST “invariant” rule at every node:

• All values in the left subtree are less than the node’s data

• All values in the right subtree are greater than the node’s data

We call a tree that has equal number of nodes to on the left and right sides “balanced”.

Visually, a small BST might look like:

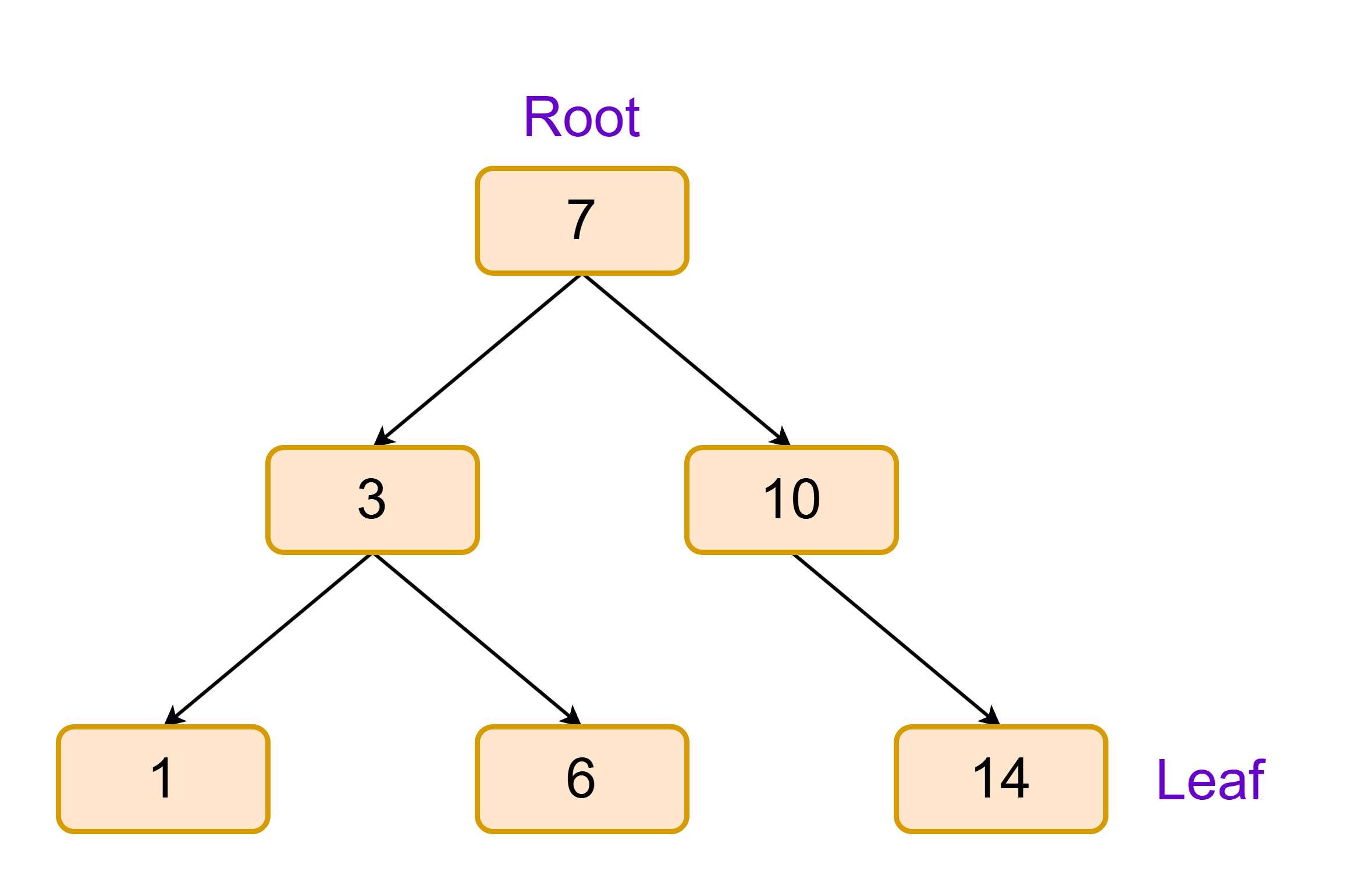
Here, for example, every value in the subtree under \(3\) is \(< 8>\), and every value under \(10\) is \(>8\).

Time Complexity

Search

To search for a value (key) we start at the root node then recurse left or right depending on the value of the node. A sketch of this process is below:

def search(node, key):
    if key == node.data:
        return True        # found
    elif key < node.data:
        return search(node.left, key)
    else:
        return search(node.right, key)

Searching is just following a single path from the root to the leaf node. Therefore it takes \(h\) steps where \(h\) is the height of the tree. To determine the time complexity for searching we need to know how \(n\) relates to \(h\).

In a balanced tree with \(n\) elements the relationship is

\[n = 1 + 2 + 4 + \dots + 2^h = 2^{h+1} - 1\]

Solving for \(h\):

\[2^{h+1} = n + 1\]

Applying log rules

\[h + 1 = \log_2 (n+1) h = \log_2 (n+1) - 1\]

Applying Big-O rules we arrive at a time complexity of \(O(\log n)\).

Insertion and Deletion

To insert a new value (key) into or delete a value from the tree we complete a search. Therefore the time complexity is related to the height of the tree and is the same as searching.

To insert a new value (key) we do the following:

1. Start at the root.

2. Compare the new key k to node.data.

3. Recurse:

   1. If k < node.data, go left;

   2. If k > node.data, go right.

4. Insert a new leaf node when you reach a None spot.

To delete a value (key) we do the following:

1. Search until you find the value

2. Perform one of the following based on the situation

   1. Leaf node: drop the key from the tree by setting its parent to None

   2. One child: assign the child to the target parent’s left or right node

   3. Two children:

      1. Find the target’s successor or predecessor

      2. Overwrite the target value with successor/predecessor value

      3. Delete successor/predecessor

Space Complexity

A BST stores exactly one node per element, and each node holds:

The data value

• Left child reference

• Right child reference

Therefore total memory requirements are \(3 \times n\) pieces of data. This simplifies to \(O(n)\).

Code Challenge: Binary Search Tree

Using the modified Node class provided, complete the BinarySearchTree class. This class will only support insertion and searching.

BinarySearchTree Specifications

Attributes

• root, a reference to the root Node of the tree

Methods

• insert(self, key), to insert the key into the tree

• search(self, key), returns True if key is in the tree, False otherwise

Each of these methods needs to recursively search, which is handled by “private” methods (starting with _).

Instructions

Note

Look for the TODO items in the provided code!

1. Check the new Node class, it now has left and right attributes for child nodes

2. Complete the recursive _search_rec(self, node, key) method to handle the cases

   1. node is None: return False since we reached the end of a branch and did not find the key

   2. node.data matches key: return True since we found a match

   3. node.data > key: recurse to the right

   4. node.data < key: recurse to the left

Usage Example

>>> bst = BinarySearchTree()
>>> bst.insert(7)
>>> bst.insert(3)
>>> bst.insert(9)
>>> bst.search(5)
False
>>> bst.search(3)
True

Here is some code for you to start with:

class Node:
    def __init__(self, d):
        self.data = d
        self.left = None
        self.right = None

    def __eq__(self, o):
        return self.data == o.data

class BinarySearchTree:
    def __init__(self):
        self.root = None

    def insert(self, key):
        self.root = self._insert_rec(self.root, key)

    def _insert_rec(self, node, key):
        # If we've hit an empty spot, put the new node here
        if node is None:
            return Node(key)

        # Otherwise recurse left or right
        if key < node.data:
            node.left = self._insert_rec(node.left, key)
        elif key > node.data:
            node.right = self._insert_rec(node.right, key)

        # key == node.data, do nothing to avoid duplication
        return node

    def search(self, key):
        return self._search_rec(self.root, key)

    def _search_rec(self, node, key):

        # TODO

bst = BinarySearchTree()

# Insert elements one by one
for value in [7, 3, 9, 1, 5, 8, 10]:
    bst.insert(value)

result = bst.search(5)
if result:
    print("Found the value in the tree!")

Solution

Solution is locked