2.4. Building a Polynomial Regression Model

To construct the 2D array required as input to our polynomial regression model we can use PolynomialFeatures from sklearn.preprocessing. We import it with the following:

from sklearn.preprocessing import PolynomialFeatures

Then we create a PolynomialFeatures object:

poly = PolynomialFeatures(degree, include_bias=False)

We set include_bias to False. bias is another word for intercept and our linear regression model will automatically calculate the intercept for us.

Finally, we pass in the input variable we’re interested in.

X = poly.fit_transform(x)

Note

x must be a 2D array with n rows, one for each sample in the dataset and 1 column. An easy way to achieve this is to use .reshape(-1, 1)

Here’s a quick example of how it works on an array containing the values [1, 2, 3, 4, 5]. You’ll notice that the first column is \(x\), the second column is \(x^2\) and the third column is \(x^3\).

from sklearn.preprocessing import PolynomialFeatures
import numpy as np

x = np.array([1, 2, 3, 4, 5])

poly = PolynomialFeatures(3, include_bias=False)
X = poly.fit_transform(x.reshape(-1, 1))

print(X)

Output

[[  1.   1.   1.]
[  2.   4.   8.]
[  3.   9.  27.]
[  4.  16.  64.]
[  5.  25. 125.]]

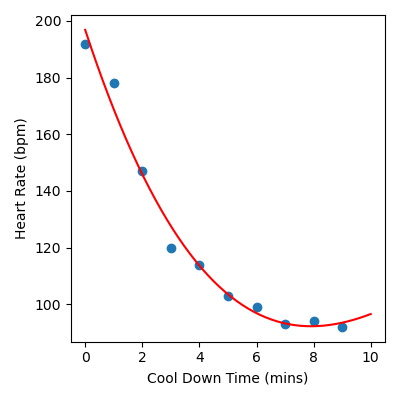
The following is a complete example of how we would fit a polynomial model of degree 3 to our heart rate during cool down time data, which is stored in cool_down.csv. You will notice that the code is very similar to the code we used to build our linear regression model.

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

# Load data
data = pd.read_csv("cool_down.csv")
x = data["Cool Down Time (mins)"].to_numpy()
y = data["Heart Rate (bpm)"].to_numpy()

# Build polynomial regression model
poly = PolynomialFeatures(3, include_bias=False)
X = poly.fit_transform(x.reshape(-1, 1))
linear_reg = LinearRegression()
linear_reg.fit(X, y)

# Create x and y values to visualise the model function
x_model = np.linspace(0, 10).reshape(-1, 1)
X_model = poly.fit_transform(x_model)
y_model = linear_reg.predict(X_model)

# Visualise the results
plt.figure(figsize=(4, 4))
plt.scatter(x, y)
plt.plot(x_model, y_model, color="red")
plt.xlabel("Cool Down Time (mins)")
plt.ylabel("Heart Rate (bpm)")
plt.tight_layout()
plt.savefig("plot.png")

Output

Code Challenge: Visualise the Data

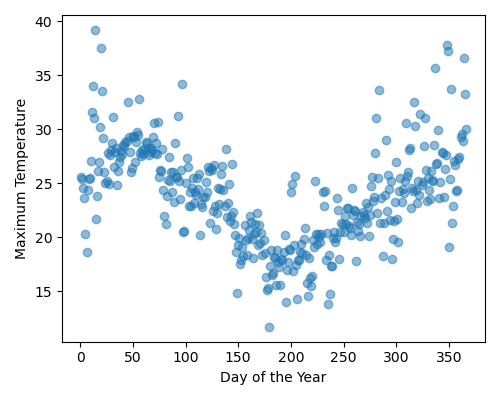
You have been provided with a csv file called sydney_temps.csv with data obtained from Kaggle . This data contains the following columns:

• Days

• MaxTemp

We will use this data to build a polynomial regression model that can help predict the maximum temperature (in degrees Celsius) for a given day of the year in Sydney.

Instructions

1. Using pandas, read the file sydney_temps.csv into a DataFrame

2. Extract the 'Day' column into the variable x

3. Extract the 'MaxTemp' column into the variable y

4. Convert both x and y to numpy arrays

5. Produce a figure that visualises the data. The figure should:

   • have figsize (5, 4)

   • plots the data as a scatter plot, alpha = 0.5

   • Have labels Day of the Year and Maximum Temperature

Your plot should look like this:

Solution

Solution is locked

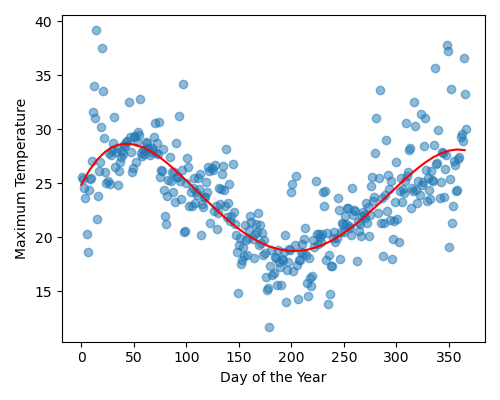
Code Challenge: Polynomial Degree 4

Now we’ll build a polynomial regression model of degree 4.

Instructions

1. Copy and paste your code from the ‘Visualise the Data’ challenge

2. Using sklearn, create a PolynomialFeatures object and use it to construct a 2D array with columns corresponding to \(x\), \(x^2\), \(x^3\) and \(x^4\).

3. Using sklearn, create a LinearRegression model and fit it to the Sydney temperature data

4. Calculate the x and y values to plot the function associated with the polynomial regression model

   • Use np.linspace(0, 365) to create the x values

   • Use .predict() to create a corresponding set of y values

5. Produce a figure that:

   • Plots the data as a scatter plot as in the ‘Visualise the Data’ challenge

   • Plots the polynomial regression model as a line, in red

Your plot should look like this:

Solution

Solution is locked