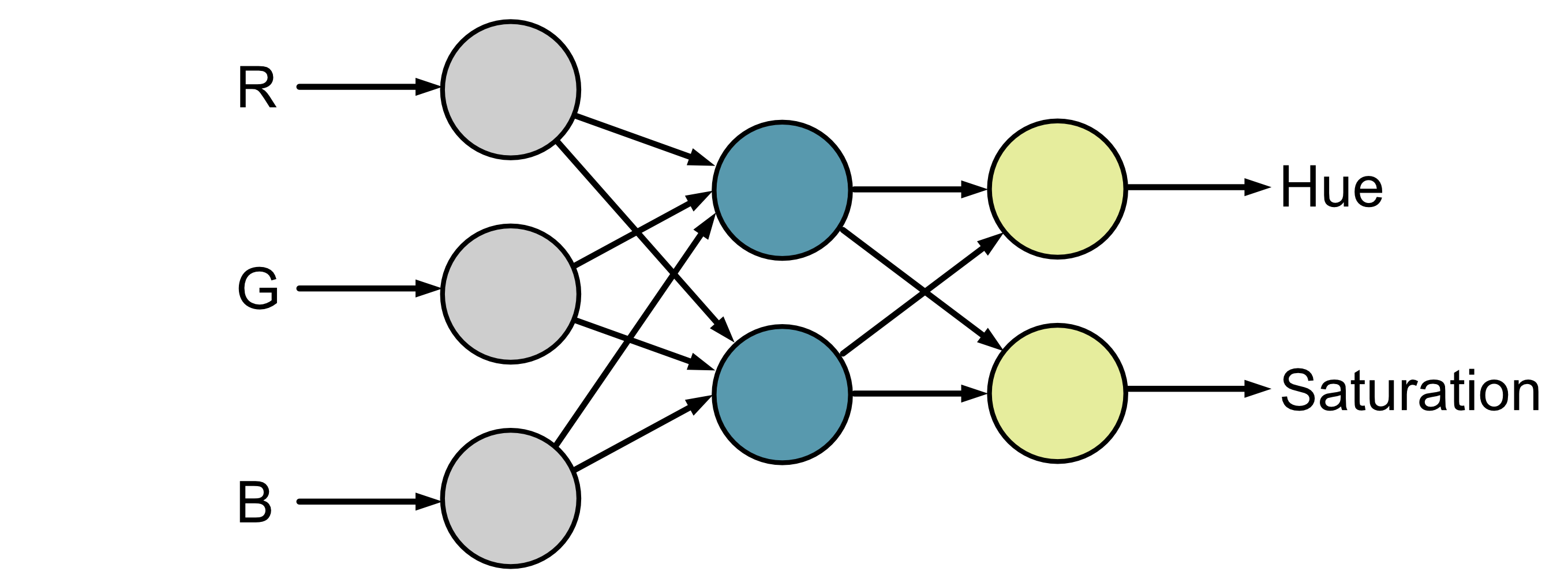
5.5. Calculating Errors#
Recall that our aim was to solve the following problem:
Given the RGB values for a colour, calculate the corresponding hue and saturation.
This is what our neural network predicted a hue of 107 and a saturation of 32 for the input (150, 25, 150).
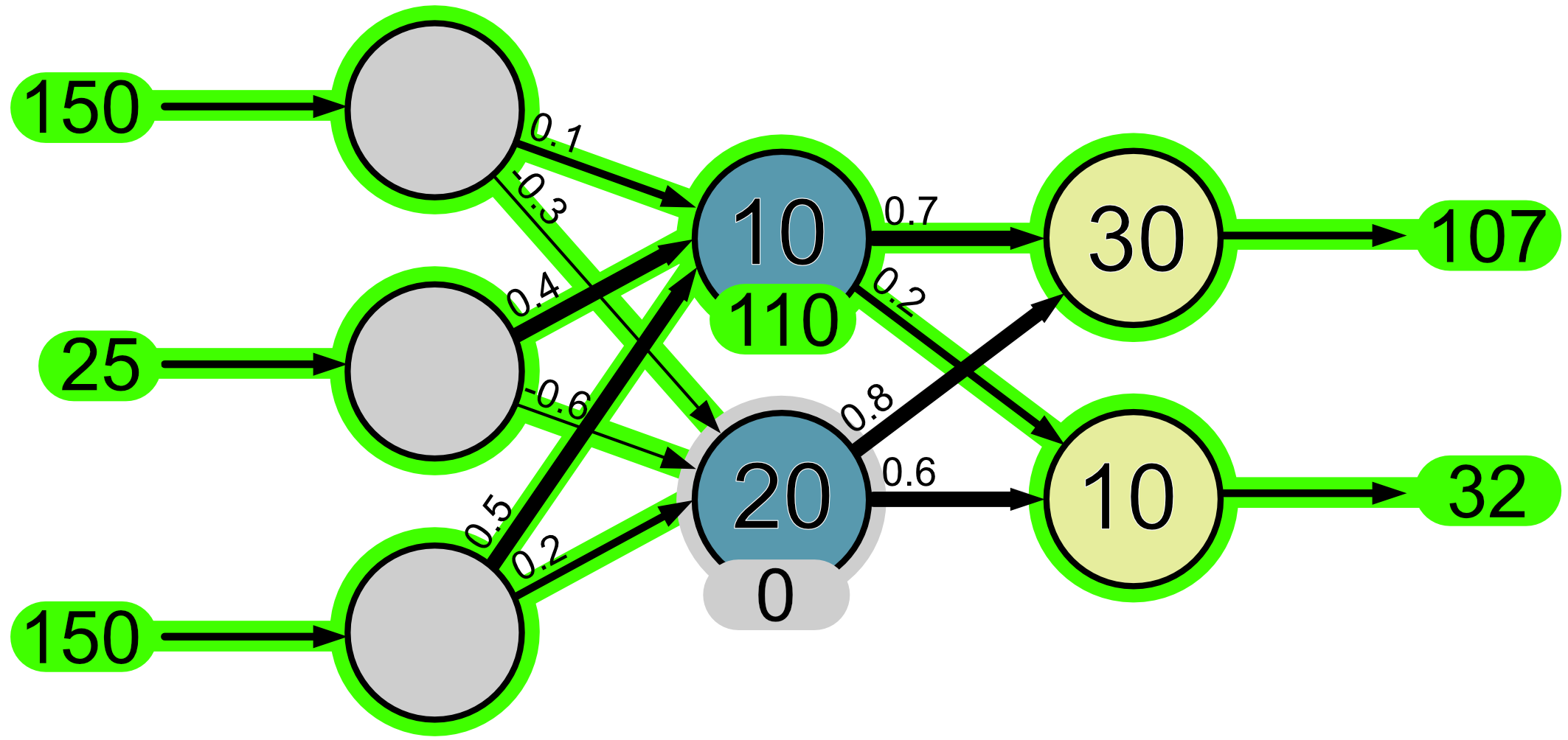
Is this correct? No it isn’t. You can see that what we wanted was a hue of 300 and a saturation of 71.
Let’s try another input.
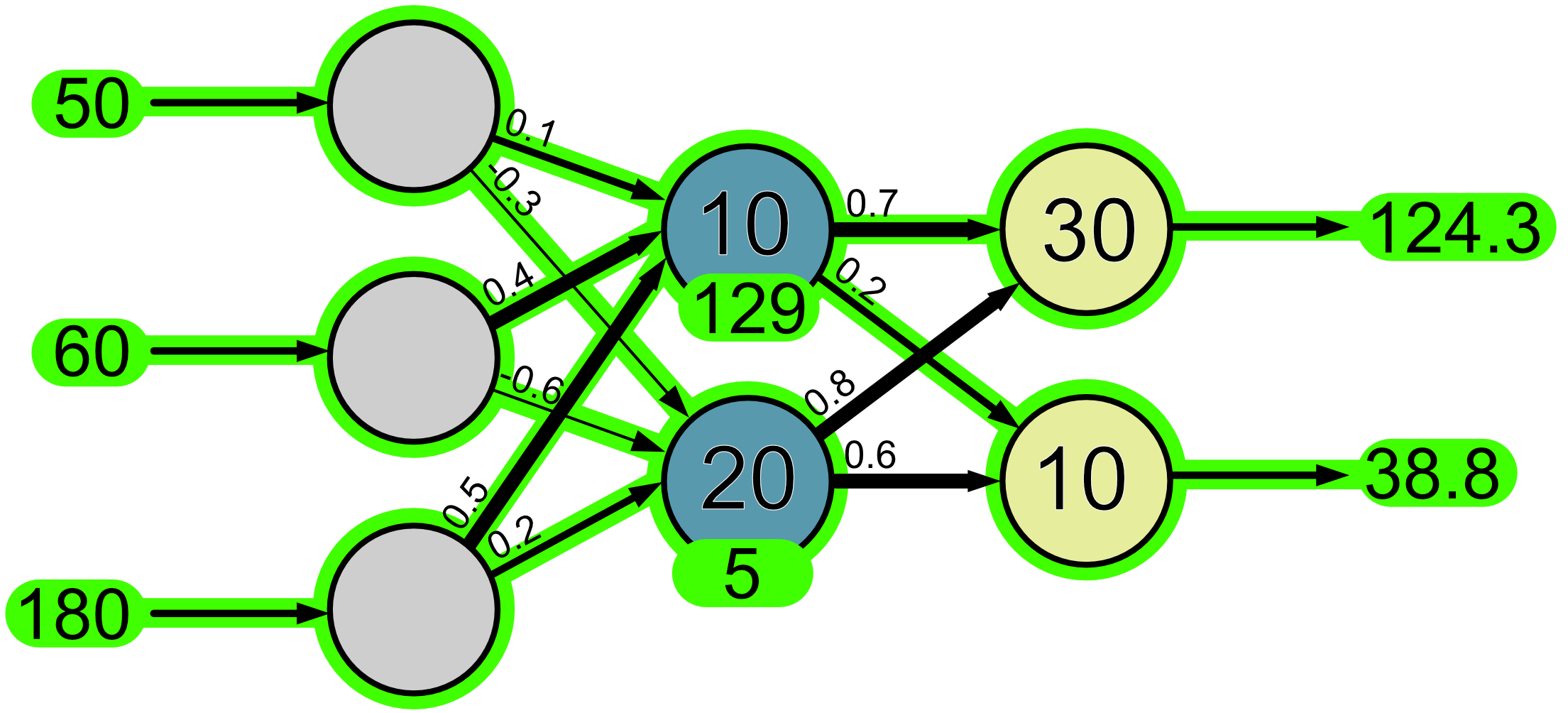
Again, it’s not quite correct. The network predicted a hue of 124.3 and a saturation of 38.8, but what we wanted was a huge of 235 and a saturation of 57.
Let’s try one more!
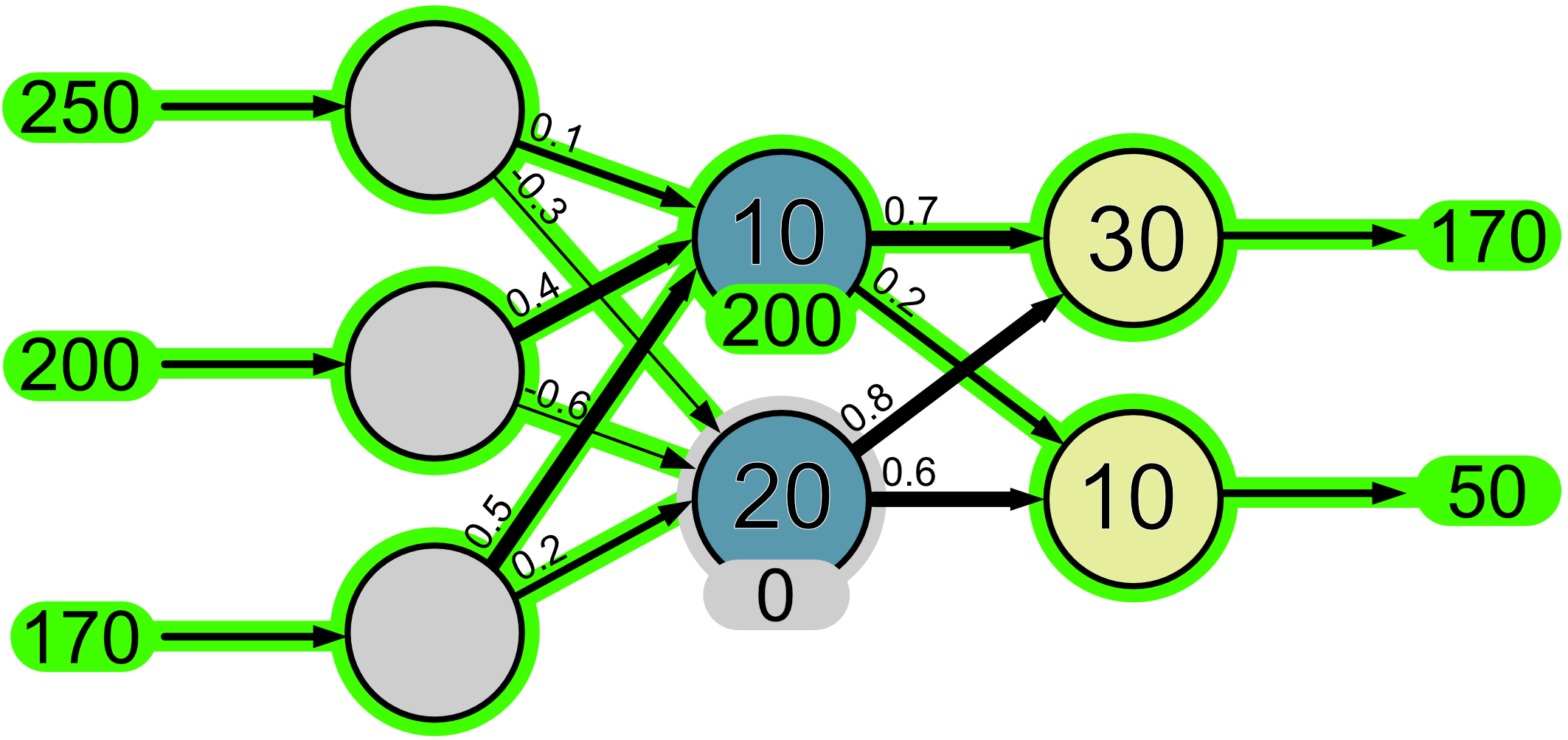
Again, it’s still not correct. The network predicted a hue of 170 and a saturation of 50, but what we wanted was a huge of 23 and a saturation of 89.
Let’s calculate the error for each sample. Since we predict two values, we calculate the error for both values in each sample.
Sample |
Predicted |
Actual |
Error (Predicted - Actual) |
|---|---|---|---|
(150, 25, 150) |
(107, 32) |
(300, 71) |
(-193, -39) |
(50, 60, 180) |
(124.3, 38.8) |
(235, 57) |
(-110.7, -18.2) |
(250, 200, 170) |
(170, 50) |
(23, 89) |
(147, -39) |
Now we’ll calculate the mean squared error across all samples. This means we take all the error values, square them and then take the average.