Fitting a Linear Regression Model

1.8. Fitting a Linear Regression Model#

We are going to learn how to fit a linear regression model using sklearn. You can read about sklearn’s linear regression model here.

We can import the function we need using the following:

from sklearn.linear_model import LinearRegression

Then we create a model:

linear_reg = LinearRegression()

Next, we give the model some data to fit. This is equivalent to the computer drawing a line of best fit to the data.

linear_reg.fit(x, y)

Note

x: must be a 2D array with \(n\) rows, one for each sample in the dataset and 1 column. An easy way to achieve this is to use .reshape(-1, 1). This means -1 rows and 1 column. The -1 will act as a place holder, and numpy will work out how many rows is required based on the specified number of columns, i.e. the data will automatically be reshaped into a column of data.
y: must be a 1D array with \(n\) values, one for each sample in the dataset

We can then extra the intercept (\(\beta_0\)) and gradient (\(\beta_1\)) of our model using:

linear_reg.intercept_
linear_reg.coef_[0]

Note

.coef_ is a list. This means that you will need to use .coef_[0] to extract out the value of :math”beta_0. Here’s an example of how we do this with our study dataset.

from sklearn.linear_model import LinearRegression
import pandas as pd

data = pd.read_csv("study.csv")

x = data["Time Spent Studying (hours)"].to_numpy()
y = data["Exam Mark (%)"].to_numpy()

linear_reg = LinearRegression()
linear_reg.fit(x.reshape(-1, 1), y)

print(linear_reg.intercept_)
print(linear_reg.coef_[0])

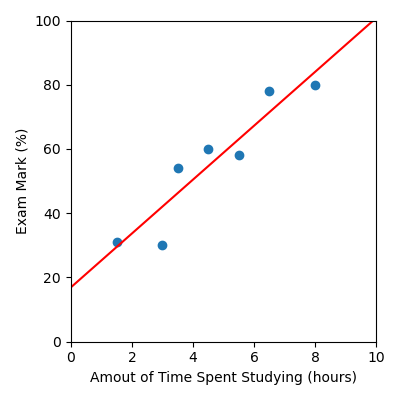
In this example the intercept is approximately 17, and the gradient is approximately 8, this means our linear regression model can be described by the mathematical equation:

\[y = 17 + 8x\]

This is what our model looks like: